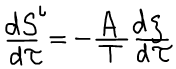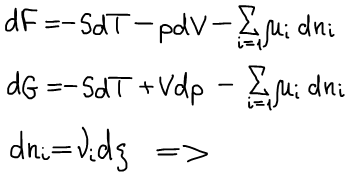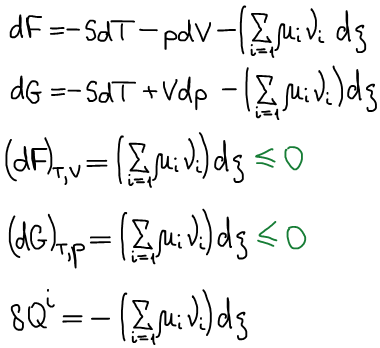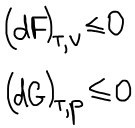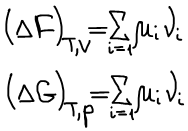Характеристические функции
Характеристическая функция — такая термодинамическая функция, по изменению которой в определенных условиях можно судить о направленности самопроизвольного процесса и о достижении состояния равновесия, а производные различного порядка которых дают нам явно и наиболее просто другие термодинамические функции и параметры системы.
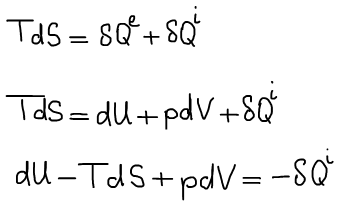
Изоэнтропийно-изохорические условия:
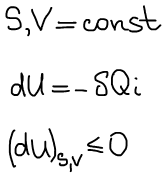
Рассмотрим только обратимые процессы.
1. Докажем, что внутренняя энергия является характеристической функцией.
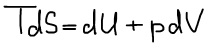
Термодинамический вид уравнения полного дифференциала внутренней энергии:
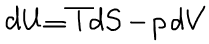
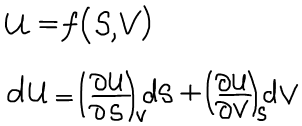
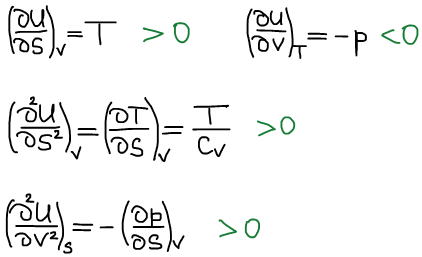
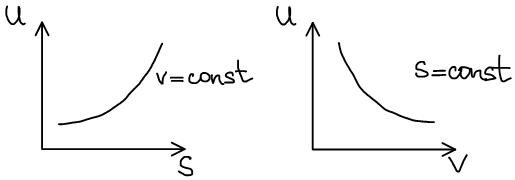
Термодинамическая система находится в состоянии истинного термодинамического равновесия при всех изменениях, совместимых с данными закрепленными значениями S и V, когда внутренняя энергия не уменьшается (либо остается постоянной, либо возрастает).
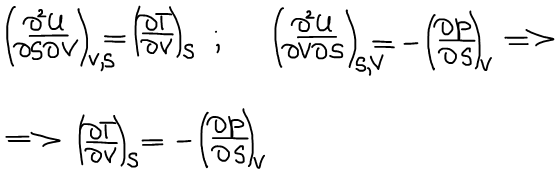
Первое уравнение Максвелла:
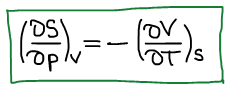
Таким образом, из приведенных выше рассуждений следует, что внутренняя энергия является характеристической функцией.
2. Докажем, что энтальпия является характеристической функцией.
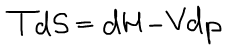
Термодинамический вид полного дифференциала энтальпии:
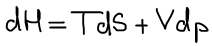
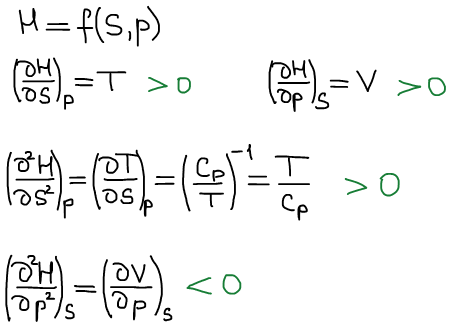
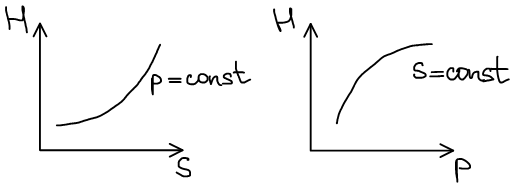
Термодинамическая система находитя в состоянии истинного термодинамического равновесия при всех изменениях совместимых с данными закрепленными значениями S и p, когда энтальпия системы не уменьшается (либо H=const, либо энтальпия возрастает). Возрастание возможно в результате флуктуаций, где флуктуация — это такое изменение, которое не является термодинамическим процессом.
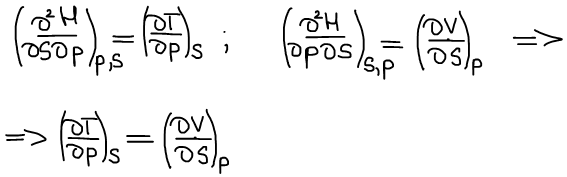
Второе уравнение Максвелла:
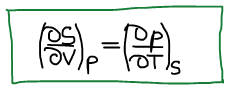

Энтальпия является характеристической функцией.
3. Докажем, что функция Гельмгольца является характеристической.
То что функция Гельгольца удовлетворяет первой части определения характеристической функции мы уже показали в 1 параграфе. Рассмотри только обратимые процессы.

Термодинамический вид уравнения полного дифференциала для функции Гельмгольца:

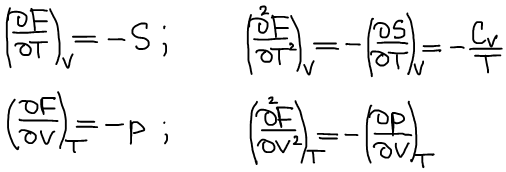
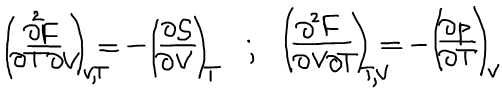
Третье уравнение Максвелла:
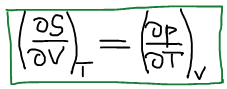
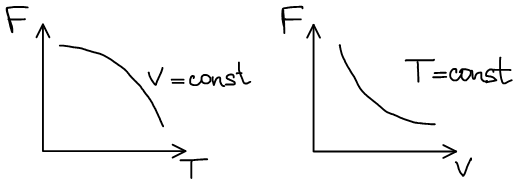
Термодинамическая система, находится в состоянии истинного термодинамического равновесия при всех изменениях, совместимых с данными закрепленными значениями T и V, когда функция Гельмгольца не уменьшается (либо остается постоянной, либо возрастает).
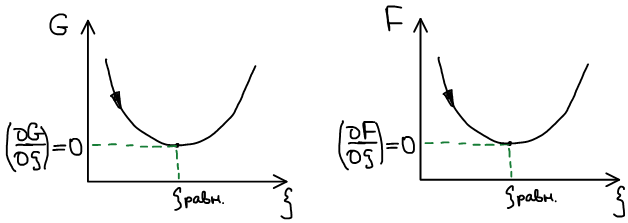
4. Докажем, что функция Гиббса является характеристической
То, что функция Гиббса удовлетворяет первой части определения характеристической функции мы показали в 1 параграфе.

Термодинамический вид уравнения полного дифференциала для функции Гиббса:
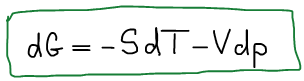
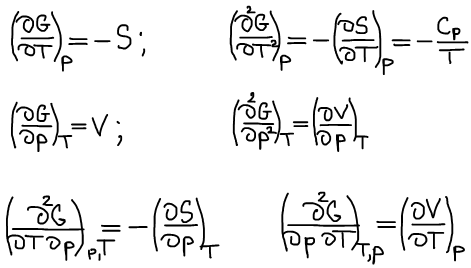
Четвертое уравнение Максвелла:
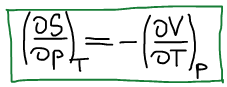
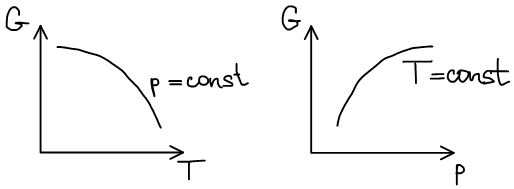
Термодинамическая система, находится в состоянии истинного термодинамического равновесия при всех изменениях, совместимых с данными закрепленными значениями T и p, когда функция Гиббса не уменьшается (либо остается постоянной, либо возрастает).
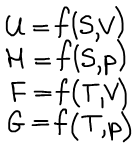
Cлучай открытой системы
Не рассматриваем протекание химических реакций, т.е. состав может изменяться только механически: за счет обмена с окружающей средой.
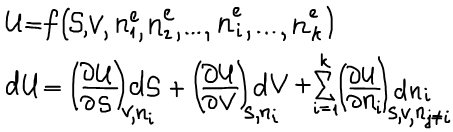
Фундаментальные уравнения термодинамики:
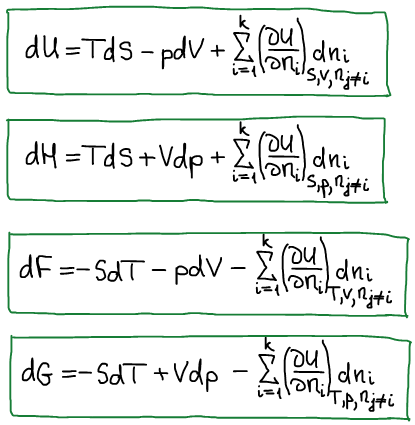
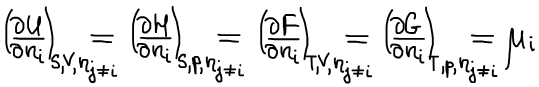
μi — химический потенциал i-го компонента — это изменение характеристической функции при внесении в систему бесконечно большого размера 1 моль i-го компонента в условиях закрепления её естественных переменных и постоянства состава.
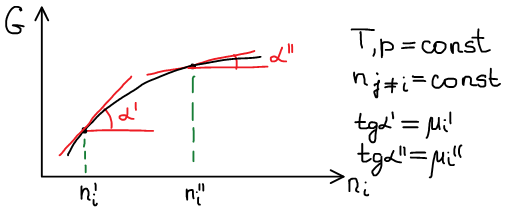
Химический потенциал i-го компонента — работа по обратимому внесению 1 моль i-го компонента в бесконечно большую систему в условиях либо изобарно-изотермических, либо изохорно-изотермических.
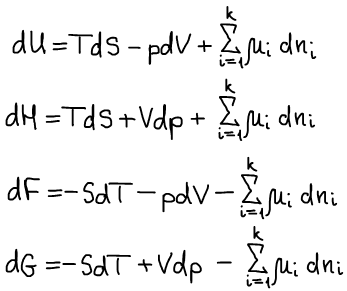
Если функция φ некоторая термодинамическая функция, то
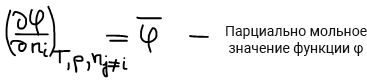
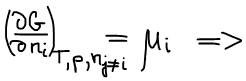
μi — парциально мольное значение функции Гиббса по i-му компоненту (справедливо только для функции Гиббса).
Cлучай закрытой системы, в которой изменение состава происходит за счет протекания химической реакции
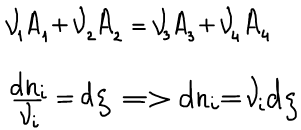
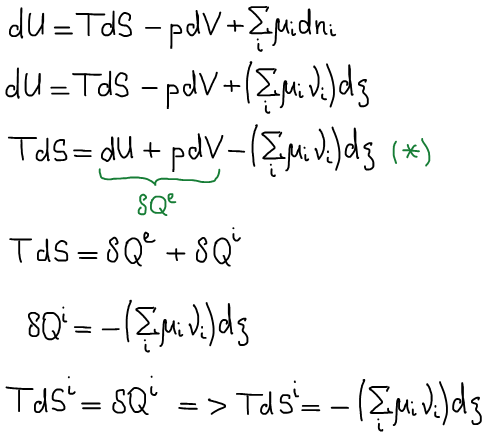
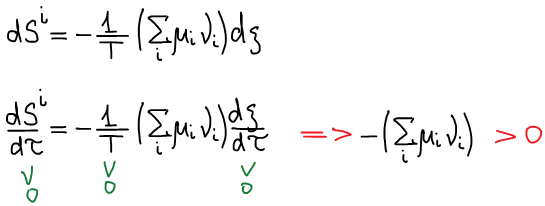

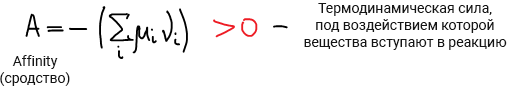
Одно из основных соотношений неравновесной термодинамики: